MATEMÁTICOS

Poluição

Trigonometria

Adição e subtração de números fracionários

Temos que analisar dois casos:

1º) denominadores iguais

Para somar frações com denominadores iguais, basta somar os numeradores e conservar o denominador.

Para subtrair frações com denominadores iguais, basta subtrair os numeradores e conservar o denominador.

Observe os exemplos:

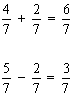
2º) denominadores diferentes

Para somar frações com denominadores diferentes, uma solução é obter frações equivalentes, de denominadores iguais ao mmc dos denominadores das frações. Exemplo: somar as frações .

Obtendo o mmc dos denominadores temos mmc(5,2) = 10.

(10:5).4 = 8

(10:2).5 = 25

Resumindo: utilizamos o mmc para obter as frações equivalentes e depois somamos normalmente as frações, que já terão o mesmo denominador, ou seja, utilizamos o caso 1.

FONTE: SÓ MATEMÁTICA

Tão visível e vivenciada quanto despercebida

A geometria se vê,
No contorno da peneira,
No formato da tv,
No gingado da capoeira,
Nas portas e nas janelas,
Na forma do pãozinho,
Nas tamancas e chinelas,
Na xícara do cafezinho,
Na fachada das casas,
Nas curvas do caminho,
Das borboletas, nas asas,
E também no meu cantinho,
Nos sólidos geométricos,
Das rochas a beira mar,
Ou nos cristais assimétricos,
Que não flutuam no ar.
A esfera que gira no espaço,
Em movimento de rotação,
Na translação está o passo,
Para a sua evolução.
E, então?
Chegamos à conclusão,
De a geometria estar,
Em todo e qualquer lugar,
Na beleza dos abrolhos,
Nas estrelas do mar,
Ou no formato dos olhos,
Que nos enchem de amor sem par,
Deus deu ao homem inteligência,
Para aprender a contar,
E evoluindo na ciência,
Sua vida melhorar,
Da geometria a importância,
Levou-o a compreender,
E diante das circunstancias
Seus cálculos desenvolver.

Ruth Nunes Dualibi